As a kid math was painfully easy. I didn't understand why people had such a hard time with it. As early as kindergarten I was correcting other kids, and have a very specific memories of teaching other kids using algebra, something my first grade teacher noticed.
So the question was 15-7=?
I'm sitting there like, ok, let me help everyone out. I asked to use the chalk board and wrote this:
7+?=10 ?=
10+?=15 ?=
I asked the other kids to solve it, and they got 3 & 5, added them together and got the answer.
The first grade teacher gave me some more problems to help show the class how to make math easier, and I helped teach math for the rest of the year. Got tested, and was sent to a magnet school... Where I then promptly hated math.
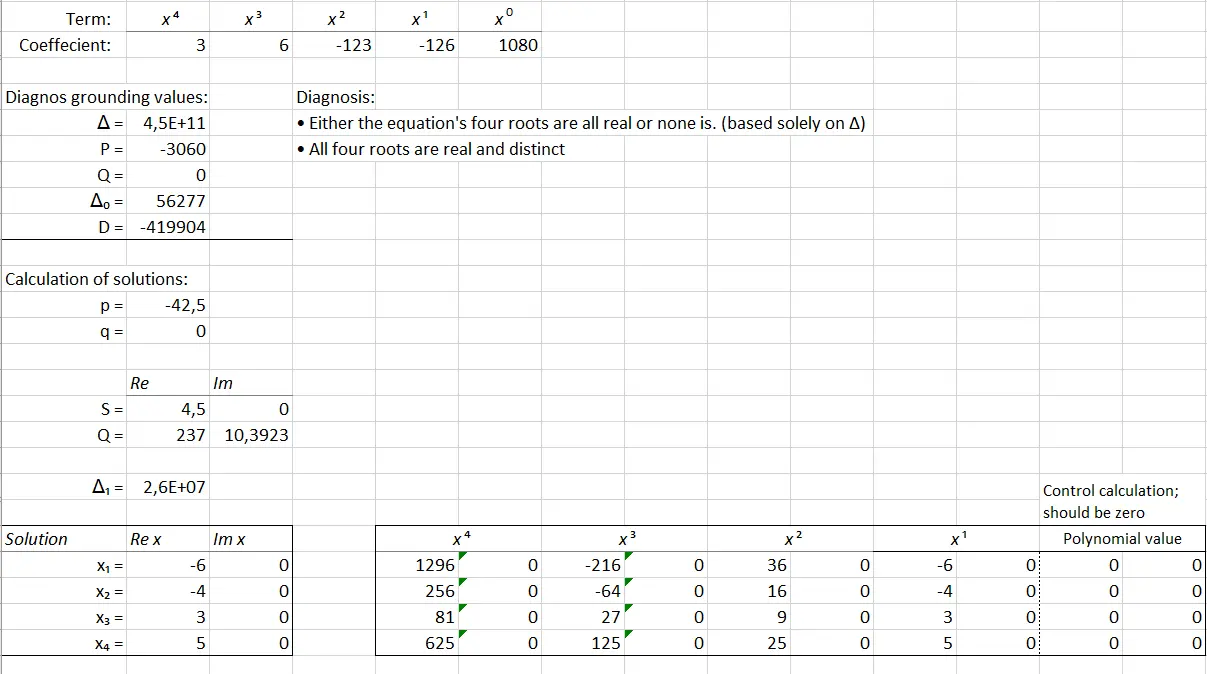
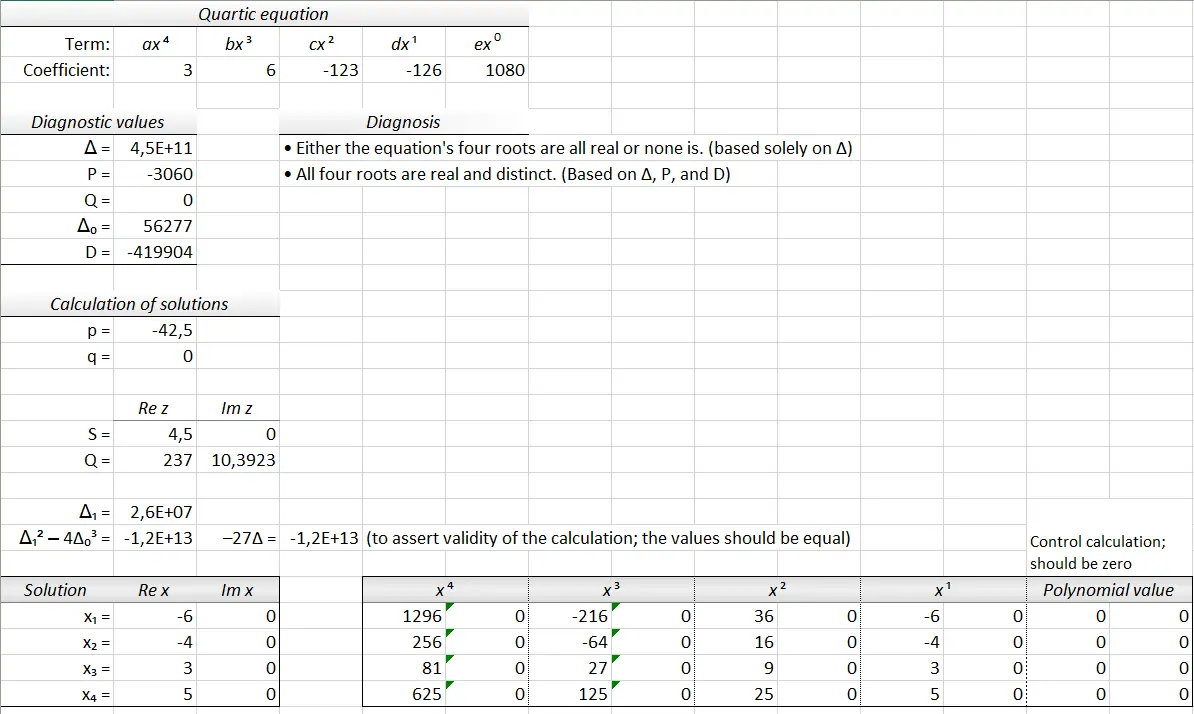
Yeah algebra is fun, graphing is like a riddle and code, but dear lord when a problem looked like this [(5-√π^x)::2]-{3,7,10}=~∆7
I'm done.
I understand it's just a new vocabulary to learn, and that math is a language unto itself, but my entire basis for understanding the world is not actually that I have some super high IQ (as outdated as that concept is) but that I excel at reducing something to it's basic points, making it easier, and rebuilding the answer.
I blame math for being easy to do in education and making me seem like a genius and putting a weight on my shoulders that grew exponentially.